Wavelet transform

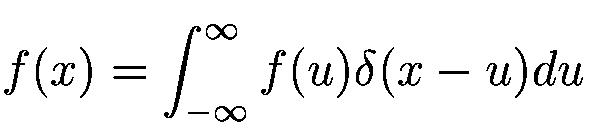
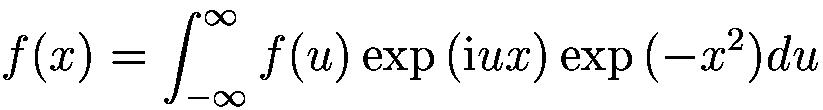
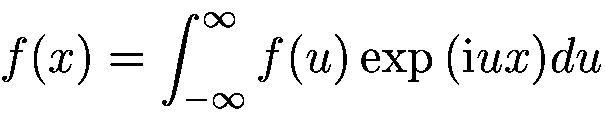
The wavelet transform is a transform similar to the Fourier transform (or much more to the windowed Fourier one as we see later) with a completely different merit function. The main difference is this: Fourier transform decomposes the signal into sines and cosines - e. g. the functions localized in Fourier space; in contrary the wavelet transform uses functions that are localized in both the real and Fourier space. The dependence on the merit function and the localization can be seen from the next table. All the mentioned transforms in the table are simply defined using convolutions with a given functions, but their meaning in terms of time and frequency resolution is different.

In the table three different similar transforms are introduced.

1. First one, a Dirac function is completely localized in the real space - transform using this function gives simply the identic function with the input signal.
2. The next merit function is a damped sine and cosine function (e. g. small wave - wavelet)- transform using this function is a mentioned Wavelet transform. As the merit function, also transform result will be localized in both the spaces.
3. Last one is the sine and cosine funcion - transform using this function is a Fourier Transform. As the merit function is localized only in the Fourier space, also the result will be.

definition	merit function in real space	merit function in Fourier space	resolution in real space	resolution in Fourier space
	Delta function	Sine and cosine	maximal; transform returns the same signal	none
	Damped sine and cosine	Shifted Gauss-like	depends on damping	depends on damping
	Sine and cosine	Delta function	none	maximal; transform returns frequency spectrum

As it is seen from the table, for the Fourier transform we don't get any resolution in real space (for time series it means the time resolution). For the stationary signals this doesn't represent any problem. As we need to analyze also non-stationary signals (most of the sounds for example), we have to use somethig else. The easiest way is to use the Short-Time Fourier Transform (or Windowed Fourier Transform).

Short-time Fourier transform simply uses a window function to choose the time area for which the frequencies are computed. Its main disadvanage is the fact that by this way we allways have: poor frequency and good time resolution for the low frequencies; good frequency and poor time resolution for the high frequencies. This is the contrary of what we usually need for the non-stationary signals.

The solution is to use the wavelet transform, which uses widows of different size for computing the high and low frequencies. Therefore, it can improve the frequency resolution of the low frequencies and the time resolution of the high frequencies. However, the uncertainity principle is valid here, so we cannot expect an improve of both time and frequency resolution for a given point in time-frequency plane; we can only vary the ratio between its time and frequency uncertainity.

The wavelet transform, which we have allready seen in the previous Table can be generally written as

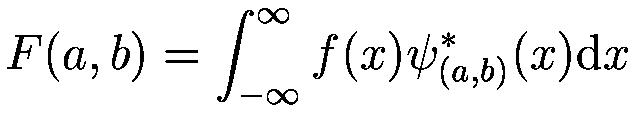
where the * is the comlex conjugate symbol and function \psi is some function which can be different obeying some rules.

Implementation of the Wavelet transform

As it is seen, the Wavelet transform is in fact an infinite set of various transforms, depending on the merit function used for its computation. This is the main reason, why we can hear the term "wavelet transform" in very different situations and applications. There are also many ways how to sort the types of the wavelet transforms. Here I show only the division based on the wavelet orthogonality.

• Orthogonal wavelets are used to develop the discrete wavelet transform
• Non-orthogonal wavelets are used to develop the continuous wavelet transform

• The discrete wavelet transform returns a data vector of the same length as the input is. Usually, even in this vector many data are almost zero. This corresponds to the fact that it decomposes into a set of wavelets (functions) that are orthogonal to its translations and scaling. Therefore we decompose such a signal to a same or lower number of the wavelet coefficient spectrum as is the number of signal data points. Such a wavelet spectrum is very good for signal processing and compression, for example, as we get no redundant information here.
• The continuous wavelet transform in contrary returns an array one dimension larger thatn the input data. For a 1D data we obtain an image of the time-frequecy plane. We can easily see the signal frequencies evolution during the duration of the signal and compare the spectrum with other signals spertra. As here is used the non-orthogonal set of wavelets, data are correlated highly, so big redundancy is seen here. This helps to see the results in a more humane form.

If you are interested in wavelets that much that you have read this page to this point, I can recomend you also to have look to the subpages (discrete wavelet transform, continuous wavelet transform, wavelet denoising and wavelet data compression), or, and this idea is much better, to have look to some good tutorial about the wavelets. Google will give you thousands of pages about this topic.

Created by Petr Klapetek, February 2002